跳转至

二叉树基础题目

约 8237 个字 1427 行代码 41 张图片 预计阅读时间 45 分钟

本篇介绍

熟悉二叉树的两种遍历方式后就可以利用二叉树的遍历来解决下面的问题

力扣2331.计算布尔二叉树的值

问题描述：

Quote

给你一棵完整二叉树的根，这棵树有以下特征：

叶子节点要么值为0要么值为1，其中 0 表示False，1 表示True。 非叶子节点要么值为2要么值为3，其中2表示逻辑或OR，3 表示逻辑与AND。 计算一个节点的值方式如下：

如果节点是个叶子节点，那么节点的值为它本身，即True或者False。 否则，计算两个孩子的节点值，然后将该节点的运算符对两个孩子值进行运算。 返回根节点root的布尔运算值。

完整二叉树是每个节点有0个或者2个孩子的二叉树。

叶子节点是没有孩子的节点。

示例 1：

C++
1
2
3
4
5
6
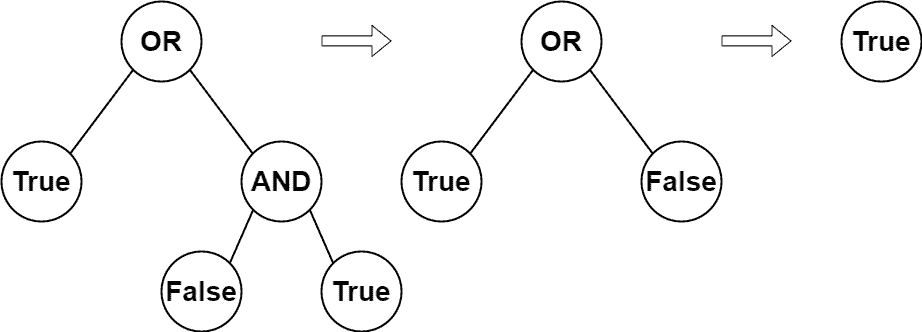
输入：root = [2,1,3,null,null,0,1]
输出：true
解释：上图展示了计算过程。
AND 与运算节点的值为 False AND True = False 。
OR 运算节点的值为 True OR False = True 。
根节点的值为 True ，所以我们返回 true 。

示例 2：

C++
1
2
3
输入：root = [0]
输出：false
解释：根节点是叶子节点，且值为 false，所以我们返回 false 。

思路分析：

使用后序遍历根据当前节点是2还是3决定何种逻辑运算符计算出左子树的布尔值和右子树的布尔值返回给对应的根节点即可

参考代码：

C++
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution2331
{
public:
    bool evaluateTree(TreeNode *root)
    {
        if (!root->left && !root->right)
            return root->val;

        bool left = 0;
        bool right = 0;
        if (root->left)
            left = evaluateTree(root->left);
        if (root->right)
            right = evaluateTree(root->right);

        if (root->val == 2)
            return (left || right);
        else if (root->val == 3)
            return (left && right);

        // 不可达，防止编译器报错
        return 0;
    }
};

力扣226.翻转二叉树

力扣226.翻转二叉树

问题描述：

Quote

给你一棵二叉树的根节点root，翻转这棵二叉树，并返回其根节点。

示例 1：

C++
1
2
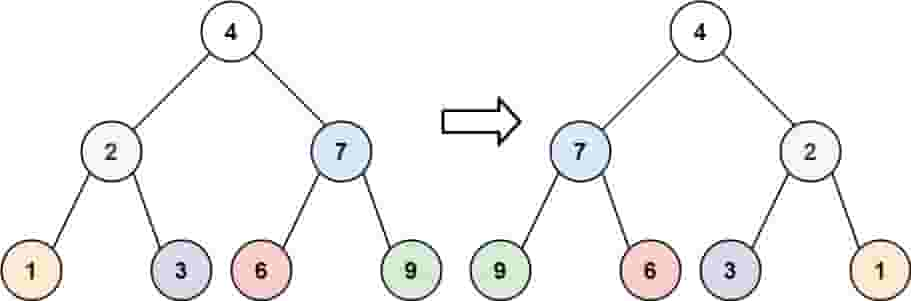
输入：root = [4,2,7,1,3,6,9]
输出：[4,7,2,9,6,3,1]

示例 2：

C++
1
2
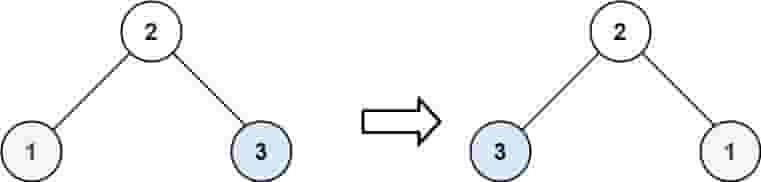
输入：root = [2,1,3]
输出：[2,3,1]

示例 3：

C++
1
2
输入：root = []
输出：[]

思路分析：

  1. 解法1：后序遍历+交换节点

    本题的基本思路的是遍历二叉树并翻转当前节点的左右孩子节点，关键的问题就是使用哪一种递归方式。首先考虑最直观的思路：先获取到左节点和右节点再进行交换，根据上面的思路可以看出，获取到左节点和右节点就是递归遍历二叉树的过程，而交换节点就是单层递归函数需要处理的逻辑，所以整体就是一个后序遍历

    基本的思路如下：

    Text Only
     1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
    以下面的二叉树为例
    4                              4
2        7         -->        7          2
1     3  6      8          8         6  3        1
后序遍历交换过程如下：
4->左->2->左->1->左->nullptr，返回nullptr到1的函数栈帧中
            1->右->nullptr，返回nullptr到1的函数栈帧中
            交换左和右，返回当前的1节点到2的函数栈帧中
    2->右->3->左->nullptr，返回nullptr到3的函数栈帧中
            3->右->nullptr，返回nullptr到3的函数栈帧中
            交换左和右，返回当前3节点到2的函数栈帧中
    交换1和3，返回当前2节点到4的函数栈帧中
    至此，左子树的子树全部翻转完毕
4->右->7->左->6->左->nullptr，返回nullptr到6的函数栈帧中
            6->右->nullptr，返回nullptr到6的函数栈帧中
            交换左和右，返回当前6到7的函数栈帧中
    7->右->8->左->nullptr，返回nullptr到8的函数栈帧中
            8->右->nullptr，返回nullptr到8的函数栈帧中
            交换左和右，返回8到7的函数栈帧中
    交换左和右，返回7到4的函数栈帧中
    至此，右子树的子树全部翻转完毕
交换左和右，返回4结束函数
至此，整棵树翻转完毕

  2. 解法2：前序遍历

    前序遍历过程中，先处理当前节点再获取左右节点，本质和后序遍历基本一致，只不过是先交换再遍历之后的子树再交换

  3. 解法3：中序遍历

    本题也可以考虑使用中序遍历，但是需要注意的是中序遍历的顺序是左中右，在本题中也就是先遍历到左节点，接着就进行交换。但是在接下来遍历右子树的时候就不难发现，上一步交换已经将原来的左节点和右节点进行了交换，此时的右子树就是原来的左子树，如果再进行交换就会回到原来的子树形式，所以下一次遍历不能遍历右子树而应该继续遍历左子树

  4. 解法4：层序遍历

    本题也可以考虑使用层序遍历，只需要在插入节点到队列前先交换节点即可

关键步骤：

本题可以考虑在交换节点时使用swap函数，但是需要注意交换的不能是局部变量，即不可以交换用变量记录的节点

参考代码：

C++
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
class Solution226_1_1
{
public:
    TreeNode *invertTree(TreeNode *root)
    {
        if (root == nullptr)
            return nullptr;

        TreeNode *left = invertTree(root->left);
        TreeNode *right = invertTree(root->right);

        // 单层函数处理逻辑
        root->left = right;
        root->right = left;

        return root;
    }
};
C++
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
class Solution226_1_2
{
public:
    TreeNode *invertTree(TreeNode *root)
    {
        if (root == nullptr)
            return nullptr;

        invertTree(root->left);
        invertTree(root->right);

        // 单层函数处理逻辑
        swap(root->left, root->right);

        return root;
    }
};
C++
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
class Solution226_2_1
{
public:
    TreeNode *invertTree(TreeNode *root)
    {
        if (root == nullptr)
            return nullptr;

        swap(root->left, root->right);
        invertTree(root->left);
        invertTree(root->right);

        return root;
    }
};
C++
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution226_2_2
{
public:
    TreeNode *invertTree(TreeNode *root)
    {

        stack<TreeNode*> st;

        st.push(root);
        while(!st.empty() && root != nullptr)
        {
            TreeNode* cur = st.top();
            st.pop();
            swap(cur->left, cur->right);
            if(cur->left)
                st.push(cur->left);
            if(cur->right)
                st.push(cur->right);
        }

        return root;
    }
};
C++
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
class Solution226_3
{
public:
    TreeNode *invertTree(TreeNode *root)
    {
        if (root == nullptr)
            return nullptr;

        invertTree(root->left);
        swap(root->left, root->right);
        invertTree(root->left);

        return root;
    }
};
C++
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution226_4
{
public:
    TreeNode *invertTree(TreeNode *root)
    {
        queue<TreeNode*> que;

        que.push(root);
        while(!que.empty() && root != nullptr)
        {
            int count = que.size();
            while(count--)
            {
                TreeNode* cur = que.front();
                que.pop();
                swap(cur->left, cur->right);
                if(cur->left)
                    que.push(cur->left);
                if(cur->right)
                    que.push(cur->right);
            }
        }

        return root;
    }
};

力扣965.单值二叉树

力扣965.单值二叉树

问题描述：

Quote

如果二叉树每个节点都具有相同的值，那么该二叉树就是单值二叉树。

只有给定的树是单值二叉树时，才返回true；否则返回false。

示例 1：

C++
1
2
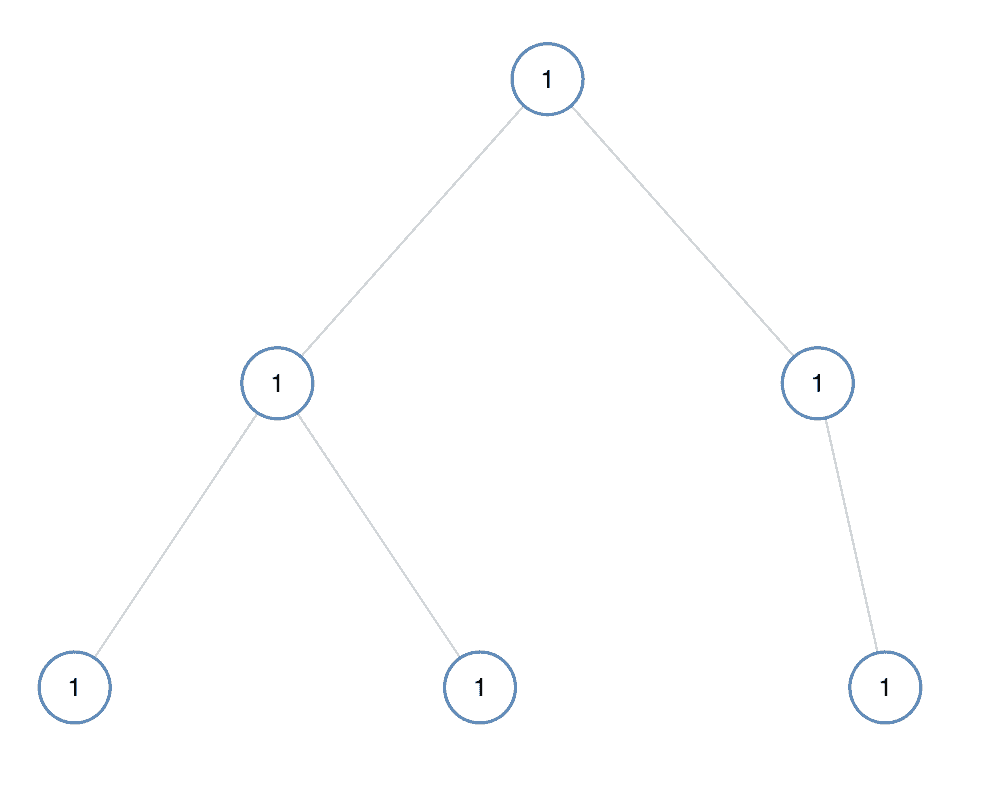
输入：[1,1,1,1,1,null,1]
输出：true

示例 2：

C++
1
2
输入：[2,2,2,5,2]
输出：false

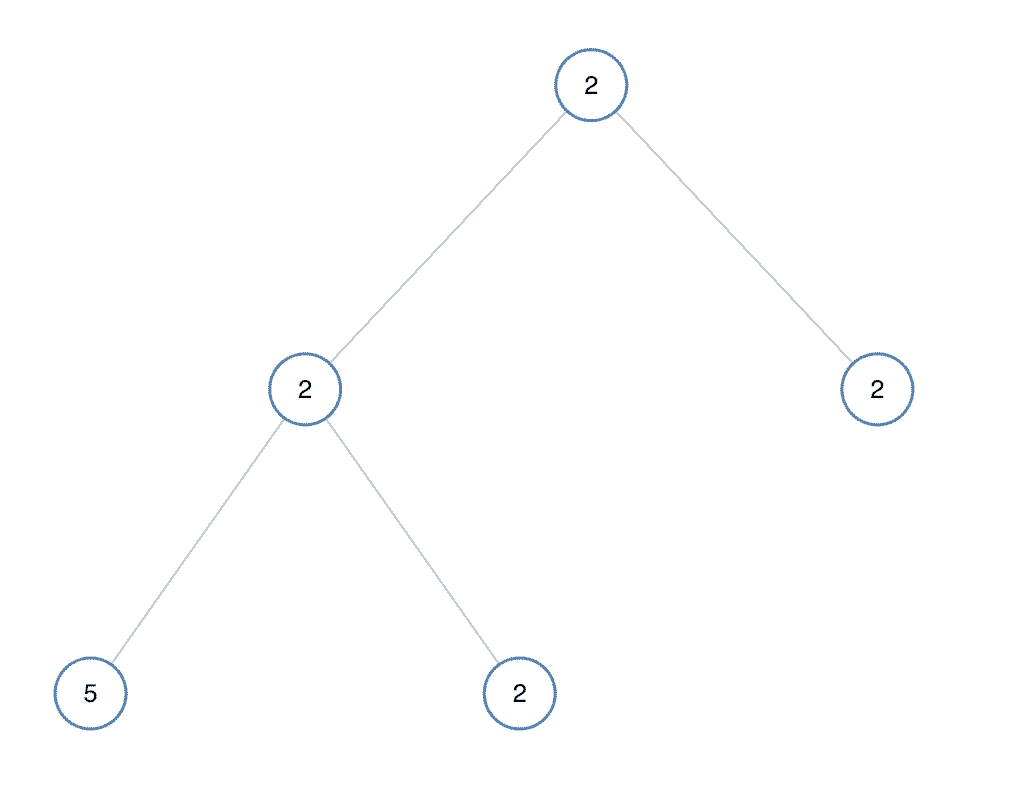
思路分析：

  1. 解法1：中序遍历

    判断当前值是否和他的左孩子和右孩子相等，如果不相等直接返回false即可，如果遍历到空节点还没有出现false，那么就说明一直都是相等的

  2. 解法2：层序遍历

    思路和中序遍历基本一致，只是通过一层一层的遍历判断每一个节点是否相同

参考代码：

C++
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
class Solution965_1
{
public:
    bool isUnivalTree(TreeNode *root)
    {
        if (!root)
            return true;

        if (root->left && root->val != root->left->val)
            return false;

        if (root->right && root->val != root->right->val)
            return false;

        return isUnivalTree(root->left) && isUnivalTree(root->right);
    }
};
C++
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
class Solution965_2
{
public:
    bool isUnivalTree(TreeNode *root)
    {
        queue<TreeNode *> que;

        que.push(root);

        while (!que.empty())
        {
            TreeNode *cur = que.front();
            que.pop();

            if (cur->left && cur->val != cur->left->val)
                return false;
            if (cur->right && cur->val != cur->right->val)
                return false;

            if (cur->left)
                que.push(cur->left);
            if (cur->right)
                que.push(cur->right);
        }

        return true;
    }
};

力扣101.对称二叉树

力扣101.对称二叉树

问题描述：

Quote

给你一个二叉树的根节点root， 检查它是否轴对称。

示例 1：

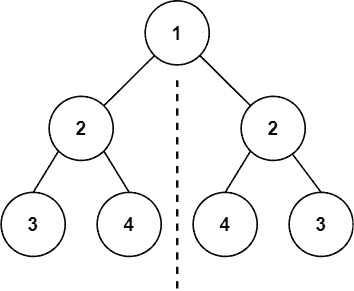
C++
1
2
输入：root = [1,2,2,3,4,4,3]
输出：true

示例 2：

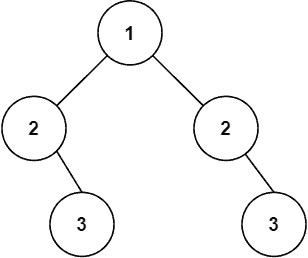
C++
1
2
输入：root = [1,2,2,null,3,null,3]
输出：false

思路分析：

判断一棵树是否是对称二叉树就是要比较左子树是否可以翻转为对应的右子树，即判断左子树的值是否等于右子树对应的值（左子树的外侧等于右子树的外侧，左子树的内侧等于右子树的内侧）

Text Only
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
以下面的二叉树为例：
          1
    2           2
3       4   4        3
最基本的思路如下：
1->左->2->左->3
 ->右->2->左->3
 相等返回true给2节点的函数栈帧
       2->右->4
       2->左->4
 相等返回true给2节点的函数栈帧
左子树的2和右子树的2返回true给1的函数栈帧

从上面的过程可以发现，需要先判断左子树的孩子和右子树的孩子是否对应一致，所以采用的遍历顺序只能是后序（左右中），因为只有后序才能满足先遍历到左右子树获取到结果，再遍历根节点向上层返回结果，并且因为需要同时获取到左孩子和右孩子，仅仅使用一个根节点肯定是不够的，所以还需要额外添加一个函数，在函数内部同时遍历两棵子树，此时就确定了函数的参数为两个，分别是左节点和右节点，因为只需要判断节点是否相等，所以返回值为布尔类型即可接着考虑递归终止条件：一共有下面几种情况： 1. 左节点为空，右节点不为空->false 2. 左节点不为空，右节点为空->false 3. 左节点和右节点都为空->true 4. 左节点和右节点的值不相等->false

上面4步中的前三步是为了排除左节点和右节点可能为空的情况

最后就是单层处理逻辑：一旦判断了左节点和右节点相等，就可以向上层返回结果，例如基本思路中的「左子树的2和右子树的2返回true给1的函数

参考代码：

C++
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class Solution101_1
{
public:
    // 同时判断两棵树
    bool _isSymmetric(TreeNode *left, TreeNode *right)
    {
        // 终止条件
        if (!left && right || left && !right)
            return false;
        else if (!left && !right)
            return true;
        else if (left->val != right->val)
            return false;

        // 遍历两棵子树的外侧
        bool outside = _isSymmetric(left->left, right->right);
        // 遍历两棵子树的内侧
        bool inside = _isSymmetric(left->right, right->left);

        // 单层处理逻辑
        return outside && inside;
    }

    bool isSymmetric(TreeNode *root)
    {
        if (!root)
            return true;
        return _isSymmetric(root->left, root->right);
    }
};
C++
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
class Solution101_2
{
public:
    bool isSymmetric(TreeNode *root)
    {
        if (!root)
            return true;
        queue<TreeNode *> que;

        que.push(root->left);
        que.push(root->right);

        while (!que.empty())
        {
            TreeNode *left = que.front();
            que.pop();
            TreeNode *right = que.front();
            que.pop();
            if (!left && right || left && !right)
                return false;
            else if (!left && !right)
                continue;
            else if (left->val != right->val)
                return false;

            // 先插入外侧
            que.push(left->left);
            que.push(right->right);
            // 再插入内侧
            que.push(left->right);
            que.push(right->left);
        }

        return true;
    }
};

力扣100.相同的树

力扣100.相同的树

问题描述：

Quote

给你两棵二叉树的根节点p和q，编写一个函数来检验这两棵树是否相同。

如果两个树在结构上相同，并且节点具有相同的值，则认为它们是相同的。

示例 1：

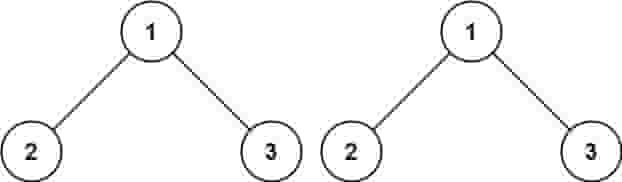
C++
1
2
输入：p = [1,2,3], q = [1,2,3]
输出：true

示例 2：

C++
1
2
输入：p = [1,2], q = [1,null,2]
输出：false

示例 3：

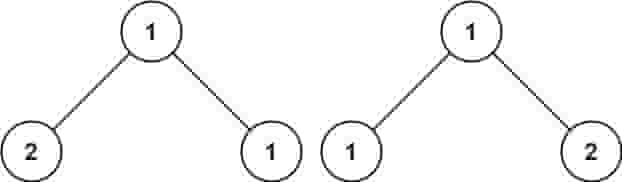
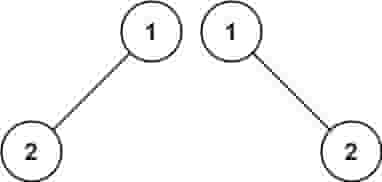
C++
1
2
输入：p = [1,2,1], q = [1,1,2]
输出：false

思路分析：

本题思路和前一题思路基本一样，只是从一棵树中判断变为了两棵树中判断，需要先比较两棵树的左右孩子再将结果返回给根节点，所以需要使用到后序遍历

参考代码：

C++
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
class Solution100
{
public:
    bool isSameTree(TreeNode *p, TreeNode *q)
    {
        if (!p && q || p && !q)
            return false;
        else if (!p && !q)
            return true;
        else if (p->val != q->val)
            return false;

        return isSameTree(p->left, q->left) && isSameTree(p->right, q->right);
    }
};

力扣572.另一棵树的子树

力扣572.另一棵树的子树

问题描述：

Quote

给你两棵二叉树root和subRoot。检验root中是否包含和subRoot具有相同结构和节点值的子树。如果存在，返回true；否则，返回false。

二叉树tree的一棵子树包括tree的某个节点和这个节点的所有后代节点。tree也可以看做它自身的一棵子树。

示例 1：

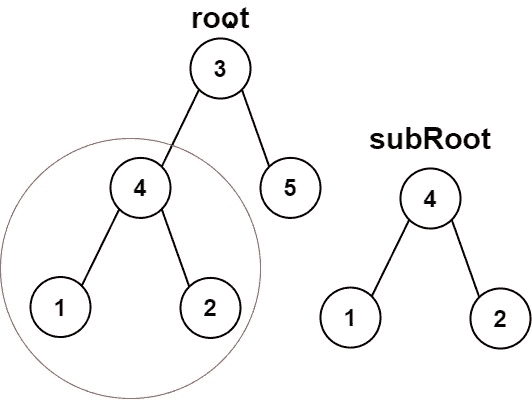
C++
1
2
输入：root = [3,4,5,1,2], subRoot = [4,1,2]
输出：true

示例 2：

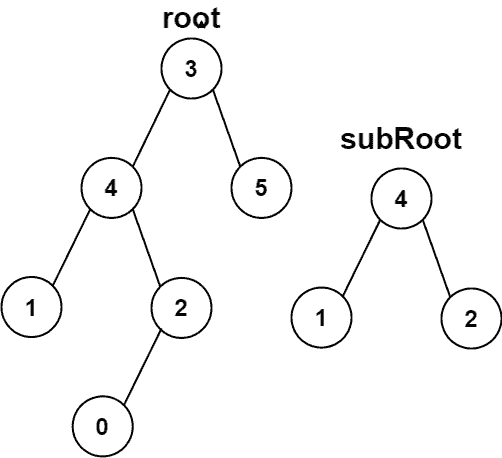
C++
1
2
输入：root = [3,4,5,1,2,null,null,null,null,0], subRoot = [4,1,2]
输出：false

思路分析：

本题判断一棵树是否是另一棵树的子树，就是判断是否存在一棵树和给定树相同，所以需要用到上一题的思路对两棵树是否相同做出判断，但是本题还需要考虑一个问题：如何在一棵完整的树中找到子树，实际上只需要将每一个节点作为根，依次判断以该根节点出发的子树是否和给定树相同

参考代码：

C++
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
class Solution572
{
public:
    bool isSameTree(TreeNode *p, TreeNode *q)
    {
        if (!p && q || p && !q)
            return false;
        else if (!p && !q)
            return true;
        else if (p->val != q->val)
            return false;

        return isSameTree(p->left, q->left) && isSameTree(p->right, q->right);
    }

    bool isSubtree(TreeNode *root, TreeNode *subRoot)
    {
        if (!root)
            return false;
        // 先判断根是否与子树相同
        if (isSameTree(root, subRoot))
            return true;

        // 再判断左子树或者右子树是否与子树相同
        return isSubtree(root->left, subRoot) || isSubtree(root->right, subRoot);
    }
};

力扣104.二叉树的最大深度

力扣104.二叉树的最大深度

问题描述：

Quote

给定一个二叉树root，返回其最大深度。

二叉树的最大深度是指从根节点到最远叶子节点的最长路径上的节点数。

示例 1：

C++
1
2
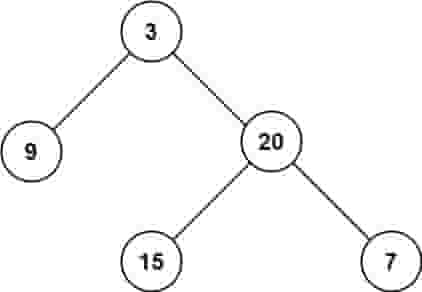
输入：root = [3,9,20,null,null,15,7]
输出：3

示例 2：

C++
1
2
输入：root = [1,null,2]
输出：2

思路分析：

  1. 解法1：后序遍历

    二叉树的最大深度实际上应该用前序遍历进行求解，而后序遍历一般用来求二叉树的高度。但是因为二叉树的最大深度就是根节点的高度，而后序遍历的思路就是将当前层的高度返回给上一层，由上一层统计当前高度，一直到根节点，此时根节点的高度就是二叉树的最大深度

  2. 解法2：层序遍历

    既然是层序遍历，那么就是按照层进行的，此时二叉树的高度就是当前二叉树的层数，只需要每遍历一层就更新层数

参考代码：

C++
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
class Solution104_1
{
public:
    int maxDepth(TreeNode *root)
    {
        if (root == nullptr)
            return 0;
        if (!root->left && !root->right)
            return 1;

        int leftHeight = maxDepth(root->left);
        int rightHeight = maxDepth(root->right);

        return leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1;
    }
};
C++
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
class Solution104_2
{
public:
    int maxDepth(TreeNode *root)
    {
        int floor = 0;
        int count = 0;
        queue<TreeNode *> que;
        que.push(root);

        while (!que.empty() && root != nullptr)
        {
            count = que.size();

            while (count--)
            {
                TreeNode *cur = que.front();
                que.pop();

                if (cur->left)
                    que.push(cur->left);

                if (cur->right)
                    que.push(cur->right);
            }

            floor++;
        }

        return floor;
    }
};

力扣559.N叉树的最大深度

力扣559.N叉树的最大深度

问题描述：

Quote

给定一个N叉树，找到其最大深度。

最大深度是指从根节点到最远叶子节点的最长路径上的节点总数。

N叉树输入按层序遍历序列化表示，每组子节点由空值分隔（请参见示例）。

示例 1：

C++
1
2
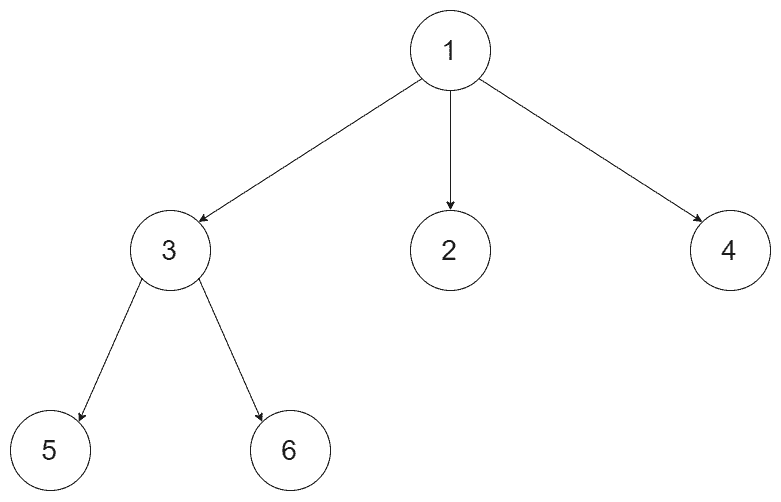
输入：root = [1,null,3,2,4,null,5,6]
输出：3

示例 2：

C++
1
2
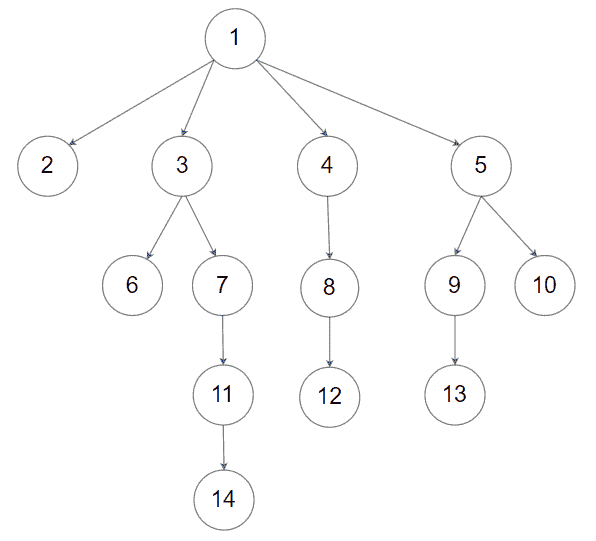
输入：root = [1,null,2,3,4,5,null,null,6,7,null,8,null,9,10,null,null,11,null,12,null,13,null,null,14]
输出：5

思路分析：

  1. 解法1：后序遍历

    本题和上一题思路基本一致，只是在处理遍历孩子节点时需要使用到循环依次获取到孩子进行遍历

  2. 解法2：层序遍历

    和上题思路一致，但是需要使用循环遍历获取孩子

参考代码：

C++
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
class Solution559_1
{
public:
    int maxDepth(Node *root)
    {
        if (!root)
            return 0;

        int depth = 0;
        for (int i = 0; i < root->children.size(); i++)
        {
            depth = max(depth, maxDepth(root->children[i]));
        }

        return depth + 1;
    }
};
C++
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class Solution559_2
{
public:
    int maxDepth(Node *root)
    {
        queue<Node *> que;
        int floor = 0, count = 0;
        que.push(root);

        while (!que.empty() && root)
        {
            count = que.size();
            while (count--)
            {
                Node *cur = que.front();
                que.pop();

                for (int i = 0; i < cur->children.size(); i++)
                {
                    que.push(cur->children[i]);
                }
            }

            floor++;
        }

        return floor;
    }
};

力扣111.二叉树的最小深度

力扣111.二叉树的最小深度

问题描述：

Quote

给定一个二叉树，找出其最小深度。

最小深度是从根节点到最近叶子节点的最短路径上的节点数量。

说明：叶子节点是指没有子节点的节点。

示例 1：

C++
1
2
输入：root = [3,9,20,null,null,15,7]
输出：2

示例 2：

C++
1
2
输入：root = [2,null,3,null,4,null,5,null,6]
输出：5

思路分析：

  1. 解法1：后序遍历

    求二叉树的最小深度只需要在二叉树的最大深度的求解过程中取出最小值即可，但是需要注意，如果左子树或者右子树不存在，此时不存在的子树高度就为0，此时0就会被当做最小高度，但是实际上此时的最小高度应该是存在的子树的高度，所以需要额外处理左子树或者右子树不存在的情况

  2. 解法2：层序遍历

    求最小深度本质就是找到最近的一个叶子结点，所以在层序遍历中第一次遇到叶子节点就返回该叶子结点的深度即可

参考代码：

C++
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
class Solution111_1
{
public:
    int minDepth(TreeNode *root)
    {
        if (!root)
            return 0;

        int leftHeight = minDepth(root->left);
        int rightHeight = minDepth(root->right);

        int depth = 0;
        if (leftHeight && rightHeight)
            depth = min(leftHeight, rightHeight);
        else if (leftHeight || rightHeight)
            depth = leftHeight ? leftHeight : rightHeight;

        return depth + 1;
    }
};
C++
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
class Solution111_2
{
public:
    int minDepth(TreeNode *root)
    {
        // 初始化时高度为1
        int count = 0, floor = 1;
        queue<TreeNode *> que;
        que.push(root);

        while (!que.empty() && root != nullptr)
        {
            count = que.size();

            while (count--)
            {
                TreeNode *cur = que.front();
                que.pop();

                if (cur->left)
                    que.push(cur->left);
                if (cur->right)
                    que.push(cur->right);

                // 找到一个叶子节点就直接返回
                if (!cur->left && !cur->right)
                {
                    return floor + 1;
                }
            }
            floor++;
        }

        return 0;
    }
};

力扣222.完全二叉树的节点个数

力扣222.完全二叉树的节点个数

问题描述：

Quote

给你一棵完全二叉树的根节点root，求出该树的节点个数。

完全二叉树的定义如下：在完全二叉树中，除了最底层节点可能没填满外，其余每层节点数都达到最大值，并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第\(h\)层（从第 0 层开始），则该层包含\(1~2^h\)个节点。

示例 1：

C++
1
2
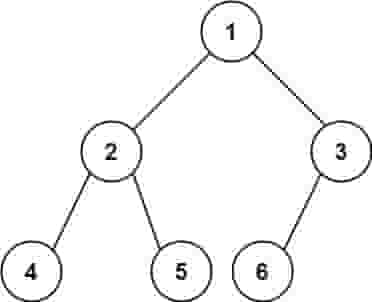
输入：root = [1,2,3,4,5,6]
输出：6

示例 2：

C++
1
2
输入：root = []
输出：0

示例 3：

C++
1
2
输入：root = [1]
输出：1

思路分析：

本题最直接的思路就是遍历整棵二叉树，遍历过程中遇到一个节点总数加1即可，但是这个做法没有用到题目给的「完全二叉树」的条件，对于一棵完全二叉树来说，可以使用公式来计算对应的满二叉树的节点个数，不是满二叉树再进行一一统计即可

参考代码：

C++
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
class Solution222_1
{
public:
    int countNodes(TreeNode *root)
    {
        if (root == nullptr)
            return 0;

        int leftNum = countNodes(root->left);
        int rightNum = countNodes(root->right);

        return leftNum + rightNum + 1;
    }
};
C++
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
class Solution222_2
{
public:
    int countNodes(TreeNode *root)
    {
        if (!root)
            return 0;

        // 是满二叉树时直接返回2^深度-1
        // 如果左子树和右子树深度相等说明当前子树是满二叉树（以完全二叉树为前提）
        int leftHeight = 0;
        int rightHeight = 0;
        TreeNode *leftNode = root->left;
        TreeNode *rightNode = root->right;
        while (leftNode)
        {
            leftHeight++;
            leftNode = leftNode->left;
        }
        while (rightNode)
        {
            rightHeight++;
            rightNode = rightNode->right;
        }

        if (leftHeight == rightHeight)
        {
            // 说明是满二叉树
            // 注意运算优先级
            return (2 << leftHeight) - 1;
        }

        // 遍历剩余子树
        leftHeight = countNodes(root->left);
        rightHeight = countNodes(root->right);

        return leftHeight + rightHeight + 1;
    }
};

力扣110.平衡二叉树

力扣110.平衡二叉树

问题描述：

Quote

给定一个二叉树，判断它是否是平衡二叉树

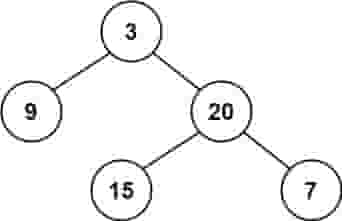
示例 1：

C++
1
2
输入：root = [3,9,20,null,null,15,7]
输出：true

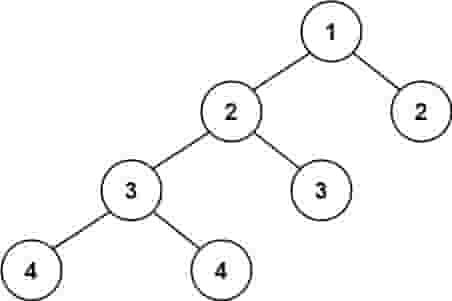
示例 2：

C++
1
2
输入：root = [1,2,2,3,3,null,null,4,4]
输出：false

示例 3：

C++
1
2
输入：root = []
输出：true

思路分析：

所谓平衡二叉树，就是该树所有节点的左右子树的高度相差不超过1。根据这个特点可以想到本题的基本思路就是获取左右子树的高度，判断差值的绝对值是否大于1，不大于就继续比较

参考代码：

C++
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class Solution110
{
public:
    // 获取二叉树高度
    int getHeight(TreeNode *root)
    {
        if (!root)
            return 0;

        int leftHeight = getHeight(root->left);
        int rightHeight = getHeight(root->right);

        return max(leftHeight, rightHeight) + 1;
    }

    bool isBalanced(TreeNode *root)
    {
        if (!root)
            return true;

        int leftHeight = getHeight(root->left);
        int rightHeight = getHeight(root->right);

        if (abs(rightHeight - leftHeight) > 1)
            return false;

        return isBalanced(root->left) && isBalanced(root->right);
    }
};

力扣257.二叉树的所有路径

力扣257.二叉树的所有路径

问题描述：

Quote

给你一个二叉树的根节点root，按任意顺序，返回所有从根节点到叶子节点的路径。

叶子节点 是指没有子节点的节点。

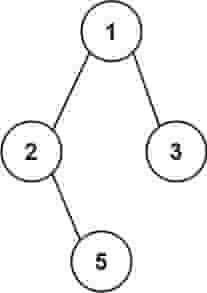
示例 1：

C++
1
2
输入：root = [1,2,3,null,5]
输出：["1->2->5","1->3"]

示例 2：

C++
1
2
输入：root = [1]
输出：["1"]

思路分析：

本题的基本思路就是遍历一个节点就向temp结构中插入该节点，记录当前节点被遍历到。如果遇到一个节点左孩子为空，右孩子也为空，则一定是叶子节点，此时就要将temp中的字符依次构成路径字符串插入到结果集中，插入完成后需要弹出当前的叶子，继续遍历右子树。此处需要注意一个细节：如果当前就是右子树，那么需要继续弹出temp中的最后一个元素，所以需要将弹出逻辑单独作为一条语句，作为向上返回前一定要执行的语句，这个过程也被称为回溯恢复现场

Text Only
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
以下面的二叉树为例
     1
  2     3
4   5
结果集：["1->2->4", "1->2->5", "1->3"]
基本思路如下：
1->左->2->左->4->左->nullptr，返回到4的函数栈帧。temp=["1", "2", "4"]
             4->右->nullptr，返回到4的函数栈帧
             判断4左右均为空，说明是叶子节点，此时将temp中的内容构成结果：1->2->4
             弹出最后一个元素。temp=["1", "2"]
             返回到2的函数栈帧
       2->右->5->左->nullptr，返回到5的函数栈帧。temp=["1", "2", "5"]
              5->右->nullptr，返回到5的函数栈帧
              判断5左右均为空，说明是叶子节点，此时将temp中的内容构成结果：1->2->5
              弹出最后一个元素。temp=["1", "5"]
              返回到2的函数栈帧
       弹出最后一个元素。temp=["1"]
       返回到1的函数栈帧
1->右->3->左->nullptr，返回到3的函数栈帧。temp=["1", "3"]
       3->右->nullptr，返回到3的函数栈帧
       判断3左右均为空，说明是叶子节点，此时将temp中的内容构成结果：1->3
       弹出最后一个元素。temp=["1"]
       返回到1的函数栈帧
弹出最后一个元素。temp=[]
回到主调函数，结束

思路优化：

实际上，本题可以将temp结构的引用去除而将其作为函数的局部变量，此时就可以不需要使用到pop_back()，因为函数在返回时已经恢复了属于其栈帧空间中的局部变量

另外，本题可以将temp结构改为普通的string，同样对于叶子节点单独处理就可以

参考代码：

C++
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
class Solution257_1
{
public:
    void addchar(TreeNode *root, vector<string> &ret, vector<string> &temp)
    {
        if (!root)
            return;

        temp.push_back(to_string(root->val));
        addchar(root->left, ret, temp);
        addchar(root->right, ret, temp);

        if (!root->left && !root->right)
        {
            string backup = "";
            for (int i = 0; i < temp.size(); i++)
            {
                backup += temp[i];
                if (i != temp.size() - 1)
                    backup += "->";
            }
            ret.push_back(backup);
        }
        temp.pop_back();
    }

    vector<string> binaryTreePaths(TreeNode *root)
    {
        vector<string> ret;
        vector<string> temp;

        addchar(root, ret, temp);

        return ret;
    }
};
C++
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
class Solution257_2
{
public:
    void addchar(TreeNode *root, vector<string> &ret, vector<string> temp)
    {
        if (!root)
            return;

        temp.push_back(to_string(root->val));
        addchar(root->left, ret, temp);
        addchar(root->right, ret, temp);

        if (!root->left && !root->right)
        {
            string backup = "";
            for (int i = 0; i < temp.size(); i++)
            {
                backup += temp[i];
                if (i != temp.size() - 1)
                    backup += "->";
            }
            ret.push_back(backup);
        }
    }

    vector<string> binaryTreePaths(TreeNode *root)
    {
        vector<string> ret;
        vector<string> temp;

        addchar(root, ret, temp);

        return ret;
    }
};
C++
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
class Solution257_3
{
public:
    void addchar(TreeNode *root, vector<string> &ret, string temp)
    {
        if (!root)
            return;

        temp += to_string(root->val);
        // 叶子节点单独处理
        if(!root->left && !root->right)
        {
            ret.push_back(temp);
            // 直接返回不需要加上->
            return;
        }
        temp += "->";

        addchar(root->left, ret, temp);
        addchar(root->right, ret, temp);
    }

    vector<string> binaryTreePaths(TreeNode *root)
    {
        vector<string> ret;
        string temp;

        addchar(root, ret, temp);

        return ret;
    }
};

力扣404.左叶子之和

力扣404.左叶子之和

问题描述：

Quote

给定二叉树的根节点root，返回所有左叶子之和。

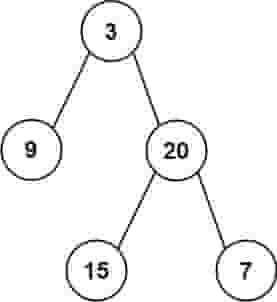
示例 1：

C++
1
2
3
输入: root = [3,9,20,null,null,15,7] 
输出: 24 
解释: 在这个二叉树中，有两个左叶子，分别是 9 和 15，所以返回 24

示例 2:

C++
1
2
输入: root = [1]
输出: 0

思路分析：

本题最直观的思路就是遍历到左孩子时再处理左孩子，但是这里会陷入一个误区：不遍历右孩子。实际上，本题除了要遍历左子树的左孩子外，也需要遍历左子树的右孩子的左孩子、右子树的左孩子和右子树的右孩子的左孩子，所以本题的思路是：遍历整棵树，但是只处理是左孩子的情况

Text Only
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
以下面的二叉树为例：
           3
     9           20
 11     21    15      7
      5
计算结果为：11+5+15=31
基本思路为：
3->左->9->左->11->左->nullptr，返回0到11的函数栈帧
              11->右->nullptr，返回0到11的函数栈帧
              返回0到9的函数栈帧
       判断11为9的左叶子，更新左叶子结果
       9->右->21->左->5->左->nullptr，返回0到5的函数栈帧
                     5->右->nullptr，返回0到5的函数栈帧
                     返回0到21的函数栈帧
             判断5为左孩子，更新左孩子结果
             21->右->nullptr，返回0到21的函数栈帧
             返回5到9的函数栈帧
        返回16到3的函数栈帧
3->右->20->左->15->左->nullptr，返回0到15的函数栈帧
              15->右->nullptr，返回0到15的函数栈帧
              返回0到20的函数栈帧
       判断15为20的左叶子，更新左叶子结果
       20->右->7->左->nullptr，返回0到7的函数栈帧
               7->右->nullptr，返回0到7的函数栈帧
               返回0到20的函数栈帧
       返回15到3的函数栈帧
返回31

参考代码：

C++
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution404
{
public:
    int sumOfLeftLeaves(TreeNode *root)
    {
        if (!root)
            return 0;
        if (!root->left && !root->right)
            // 左孩子和右孩子都会空，无法判断当前孩子一定为左孩子
            // 所以直接返回0即可
            return 0;

        // 遍历左子树
        int leftNum = sumOfLeftLeaves(root->left);
        // 判断是否是左孩子，是就处理
        if (root->left && (!root->left->left && !root->left->right))
            leftNum = root->left->val;

        // 遍历右子树
        int rightNum = sumOfLeftLeaves(root->right);
        // 虽然遍历右子树，但是右孩子都不做处理

        return leftNum + rightNum;
    }
};

力扣513.找树左下角的值

力扣513.找树左下角的值

问题描述：

Quote

给定一个二叉树的根节点root，请找出该二叉树的最底层最左边节点的值。

假设二叉树中至少有一个节点。

示例 1:

C++
1
2
输入: root = [2,1,3]
输出: 1

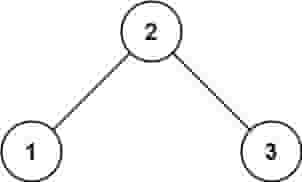
示例 2:

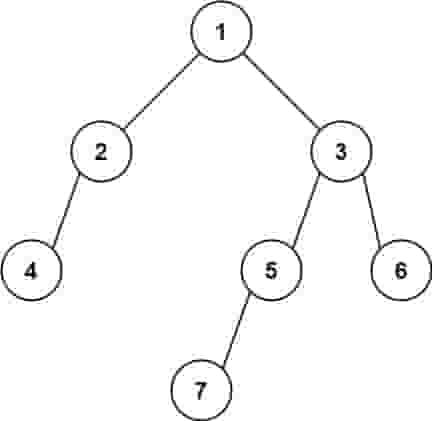
C++
1
2
输入: [1,2,3,4,null,5,6,null,null,7]
输出: 7

思路分析：

  1. 解法1：层序遍历

    本题最容易想到的解法就是层序遍历，在层序遍历中，只需要找到最底层的第一个出现的节点即可，为了防止被同层的节点覆盖，可以使用flag标记

  2. 解法2：递归遍历

    递归法就是通过求深度控制最底层，在获取到最底层时就记录节点，否则继续遍历

参考代码：

C++
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
class Solution513_1
{
public:
    int findBottomLeftValue(TreeNode *root)
    {
        if (!root->left && !root->right)
            return root->val;
        queue<TreeNode *> que;
        que.push(root);

        TreeNode *ret = nullptr;

        while (!que.empty())
        {
            int count = que.size();
            bool floor = true;
            while (count--)
            {
                TreeNode *cur = que.front();
                que.pop();

                if (cur->left && !cur->left->left && !cur->left->right && floor)
                {
                    ret = cur->left;
                    floor = false;
                }
                else if (cur->right && !cur->right->left && !cur->right->right && floor)
                {
                    ret = cur->right;
                    floor = false;
                }

                if (cur->left)
                    que.push(cur->left);
                if (cur->right)
                    que.push(cur->right);
            }
        }

        return ret->val;
    }
};
C++
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
class Solution513_2
{
public:
    int maxDepth = INT_MIN;
    int result = 0;

    void traversalWithDepth(TreeNode *root, int depth)
    {
        // 遍历到叶子节点时判断是不是最底层的叶子
        if (!root->left && !root->right)
        {
            if (depth > maxDepth)
            {
                maxDepth = depth;
                result = root->val;
            }
            return;
        }

        // 遍历左子树
        if (root->left)
        {
            depth++;
            traversalWithDepth(root->left, depth);
            // 返回调用处时会向上一层返回
            depth--;
        }

        // 遍历右子树
        if (root->right)
        {
            depth++;
            traversalWithDepth(root->right, depth);
            // 返回调用处时会向上一层返回
            depth--;
        }
    }

    int findBottomLeftValue(TreeNode *root)
    {
        if (!root->left && !root->right)
            return root->val;

        int depth = 0;
        traversalWithDepth(root, depth);

        return result;
    }
};

力扣112.路径总和

力扣112.路径总和

问题描述：

Quote

给你二叉树的根节点root和一个表示目标和的整数targetSum。判断该树中是否存在根节点到叶子节点的路径，这条路径上所有节点值相加等于目标和targetSum。如果存在，返回true；否则，返回false。

叶子节点是指没有子节点的节点。

示例 1：

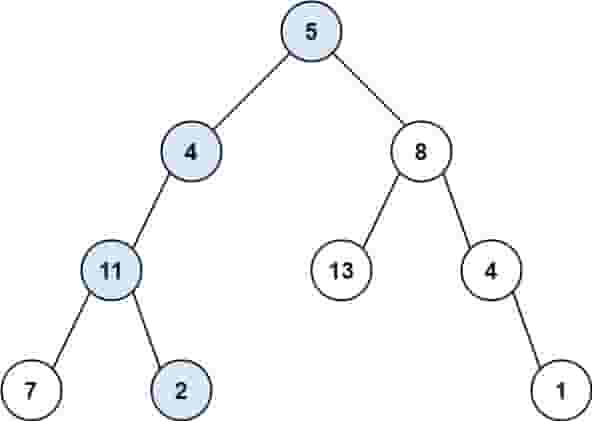
C++
1
2
3
输入：root = [5,4,8,11,null,13,4,7,2,null,null,null,1], targetSum = 22
输出：true
解释：等于目标和的根节点到叶节点路径如上图所示。

示例 2：

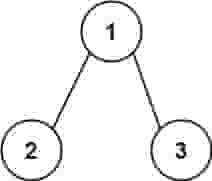
C++
1
2
3
4
5
6
输入：root = [1,2,3], targetSum = 5
输出：false
解释：树中存在两条根节点到叶子节点的路径：
(1 --> 2): 和为 3
(1 --> 3): 和为 4
不存在 sum = 5 的根节点到叶子节点的路径。

示例 3：

C++
1
2
3
输入：root = [], targetSum = 0
输出：false
解释：由于树是空的，所以不存在根节点到叶子节点的路径。

思路分析：

本题基本思路：通过sum变量的值判断是否与目标值targetSum相等，并且当前节点需要满足是叶子节点，「当前节点是叶子」在本题中尤为重要，因为存在一种情况：还没到叶子时，sum就已经和targetSum相等，或者sum大于targetSum，对于上面这两种情况，如果单独处理会非常麻烦还不容易处理，所以针对上面的思路，考虑出递归的终止条件：

  1. 当前节点是叶子节点，并且当前的sum == targetSum时，说明找到一条路径满足
  2. 当前节点是叶子节点，但是当前的sum != targetSum时，说明当前路径此时不满足

既然要判断是叶子节点，就需要判断当前节点的左孩子和右孩子都是nullptr，所以为了防止出现空指针解引用的错误，在遍历下一层时也需要判断下一层是否为空。最后就是需要考虑到sum的计算问题，因为是不同的函数栈帧，在退回时sum的值会进行改变，或者说在一个函数内对sum的修改不影响另外一个函数中的sum，所以需要考虑到sum何时需要恢复到原来的数值，给出一种思路：先遍历左子树，此时sum加上左子树节点的值，进入新的函数栈帧，如果为true直接返回，代表找到一条路径；如果为false就要走右子树，此时就需要更新sum，让其减去左子树回到没有加左子树值的状态；接着遍历右子树，此时sum也是加上右子树节点的值，进入新的函数栈帧，如果为true直接返回，代表找到一条路径；如果为false就要走右子树，此时可以考虑恢复sum，也可以不考虑，因为走到右子树还没有找到路径，说明当前子树不存在一条根节点到叶子节点的路径和为targetSum，直接返回false，此时的sum因为是在当前节点的栈帧中更新的，既然不存在满足条件的路径，那么说明当前子树一定不存在满足条件的路径，向上返回时sum还是原来的sum

参考代码：

C++
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
class Solution112
{
public:
    bool _hashPathSum(TreeNode *root, int targetSum, int sum)
    {
        if (!root->left && !root->right && sum == targetSum)
            return true;
        else if (!root->left && !root->right && sum != targetSum)
            return false;

        if (root->left)
        {
            sum += root->left->val;
            if (_hashPathSum(root->left, targetSum, sum))
                return true;

            sum -= root->left->val;
        }

        if (root->right)
        {
            sum += root->right->val;
            if (_hashPathSum(root->right, targetSum, sum))
                return true;

            // 此处的回溯可以保留也可以去掉，因为走到了这一步说明上面sum改变的值进入到右子树的栈帧空间返回的是false
            // 如果没有下面的回溯，那么走完if就直接走到了下面的return false回到上一层函数栈帧
            // 此时的sum依旧是没有加上右子树节点值的sum
            sum -= root->right->val;
        }

        return false;
    }

    bool hasPathSum(TreeNode *root, int targetSum)
    {
        if (!root)
            return false;
        else if (!root->left && !root->right && root->val == targetSum)
            return true;

        return _hashPathSum(root, targetSum, root->val);
    }
};

力扣113.路径总和Ⅱ

力扣113.路径总和Ⅱ

问题描述：

Quote

给你二叉树的根节点root和一个整数目标和targetSum，找出所有从根节点到叶子节点路径总和等于给定目标和的路径。

叶子节点是指没有子节点的节点。

示例 1：

C++
1
2
输入：root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22
输出：[[5,4,11,2],[5,8,4,5]]

示例 2：

C++
1
2
输入：root = [1,2,3], targetSum = 5
输出：[]

示例 3：

C++
1
2
输入：root = [1,2], targetSum = 0
输出：[]

思路分析：

本题和上题基本类似，不同的是，本题不是找到一条满足条件的路径就结束，而是找到所有满足条件的路径，所以不论是找到还是没有找到，都需要继续执行上层栈帧的回溯

参考代码：

C++
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
class Solution113
{
public:
    void _pathSum(TreeNode *root, int targetSum, int sum, vector<int> &temp, vector<vector<int>> &ret)
    {
        if (!root->left && !root->right && sum == targetSum)
        {
            ret.push_back(temp);
            return;
        }

        if (root->left)
        {
            sum += root->left->val;
            temp.push_back(root->left->val);
            _pathSum(root->left, targetSum, sum, temp, ret);

            sum -= root->left->val;
            temp.pop_back();
        }

        if (root->right)
        {
            sum += root->right->val;
            temp.push_back(root->right->val);
            _pathSum(root->right, targetSum, sum, temp, ret);

            sum -= root->right->val;
            temp.pop_back();
        }
    }

    vector<vector<int>> pathSum(TreeNode *root, int targetSum)
    {
        if (!root)
            return {};
        else if (!root->left && !root->right && root->val == targetSum)
            return {{root->val}};

        vector<int> temp;
        vector<vector<int>> ret;
        temp.push_back(root->val);

        _pathSum(root, targetSum, root->val, temp, ret);

        return ret;
    }
};

力扣106.从中序与后序遍历序列构造二叉树

力扣106.从中序与后序遍历序列构造二叉树

问题描述：

Quote

给定两个整数数组inorder和postorder，其中inorder是二叉树的中序遍历，postorder是同一棵树的后序遍历，请你构造并返回这棵二叉树。

示例 1:

C++
1
2
输入：inorder = [9,3,15,20,7], postorder = [9,15,7,20,3]
输出：[3,9,20,null,null,15,7]

示例 2:

C++
1
2
输入：inorder = [-1], postorder = [-1]
输出：[-1]

思路分析：

根据后序遍历找出根节点，再根据根节点分别切割前序遍历数组和后序遍历数组重复调用函数直到数组为空时代表遍历完成，每一次遍历都会在其中找出当前数组的根节点，此时的根节点就是其对应的子树的根节点，将这个根节点向上返回即可依次构造出一棵完整的二叉树

参考代码：

C++
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
class Solution106
{
public:
    TreeNode *buildTree(vector<int> &inorder, vector<int> &postorder)
    {
        if (postorder.size() == 0)
            return nullptr;
        // 1. 根据后序遍历获取根节点
        int rootVal = postorder[postorder.size() - 1];
        TreeNode *root = new TreeNode(rootVal);

        // 2. 根据根节点在中序中分左区间数组和右区间数组
        int rootIndex = 0;
        for (int i = 0; i < inorder.size(); i++)
        {
            if (inorder[i] == rootVal)
            {
                rootIndex = i;
                break;
            }
        }

        // 左闭右开原则分割
        vector<int> inorderLeft(inorder.begin(), inorder.begin() + rootIndex);
        vector<int> inorderRight(inorder.begin() + rootIndex + 1, inorder.end());

        // 3. 根据根节点在后序中分左区间数组和右区间数组
        // 先舍去后序的最后一个元素
        postorder.resize(postorder.size() - 1);
        // 左闭右开原则分割
        vector<int> postorderLeft(postorder.begin(), postorder.begin() + inorderLeft.size());
        vector<int> postorderRight(postorder.begin() + inorderLeft.size(), postorder.end());

        // 4. 根据左中和左后、右中和右后重复上述步骤
        root->left = buildTree(inorderLeft, postorderLeft);
        root->right = buildTree(inorderRight, postorderRight);

        // 5. 返回根节点
        return root;
    }
};

力扣105.从前序与中序遍历序列构造二叉树

力扣105.从前序与中序遍历序列构造二叉树

问题描述：

Quote

给定两个整数数组preorder和inorder，其中preorder是二叉树的先序遍历，inorder是同一棵树的中序遍历，请构造二叉树并返回其根节点。

示例 1:

C++
1
2
输入: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
输出: [3,9,20,null,null,15,7]

示例 2:

C++
1
2
输入: preorder = [-1], inorder = [-1]
输出: [-1]

思路分析：

本题和上题思路基本一致，只是使用的数组不同而已

思考问题：

Question

是否可以根据前序遍历和后序遍历结果唯一确定一棵二叉树？

实际上是不可以的，因为前序遍历和后序遍历本质都是确定根节点所在位置，但是此时只能在这两个数组中确定整棵树的根节点，没有办法确定其他子树的节点，所以导致结果二叉树不唯一

参考代码：

C++
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
class Solution105
{
public:
    TreeNode *buildTree(vector<int> &preorder, vector<int> &inorder)
    {
        // 检查输入数组的有效性
        if (preorder.size() == 0)
            return nullptr;

        // 获取根节点值
        int rootVal = preorder[0];
        TreeNode *root = new TreeNode(rootVal);

        // 在中序遍历中查找根节点位置
        int rootIndex = -1;
        for (int i = 0; i < inorder.size(); i++)
        {
            if (inorder[i] == rootVal)
            {
                rootIndex = i;
                break;
            }
        }

        // 分割中序数组 - 左子树
        vector<int> inorderLeft(inorder.begin(), inorder.begin() + rootIndex);
        // 分割中序数组 - 右子树
        vector<int> inorderRight(inorder.begin() + rootIndex + 1, inorder.end());

        // 分割前序数组时确保不会越界
        if (inorderLeft.size() > preorder.size() - 1)
            return nullptr;

        // 分割前序数组 - 左子树
        vector<int> preorderLeft(preorder.begin() + 1,preorder.begin() + 1 + inorderLeft.size());
        // 分割前序数组 - 右子树
        vector<int> preorderRight(preorder.begin() + 1 + inorderLeft.size(),preorder.end());

        // 递归构建左右子树
        root->left = buildTree(preorderLeft, inorderLeft);
        root->right = buildTree(preorderRight, inorderRight);

        return root;
    }
};

力扣654.最大二叉树

力扣654.最大二叉树

问题描述：

给定一个不重复的整数数组nums。最大二叉树可以用下面的算法从nums递归地构建:

  • 创建一个根节点，其值为nums中的最大值。
  • 递归地在最大值左边的子数组前缀上构建左子树。
  • 递归地在最大值右边的子数组后缀上构建右子树。
  • 返回nums构建的最大二叉树。

示例 1：

C++
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
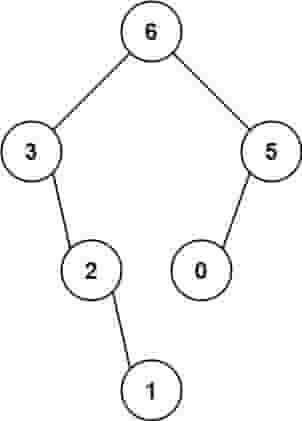
12
输入：nums = [3,2,1,6,0,5]
输出：[6,3,5,null,2,0,null,null,1]
解释：递归调用如下所示：
- [3,2,1,6,0,5] 中的最大值是 6 ，左边部分是 [3,2,1] ，右边部分是 [0,5] 。
    - [3,2,1] 中的最大值是 3 ，左边部分是 [] ，右边部分是 [2,1] 。
        - 空数组，无子节点。
        - [2,1] 中的最大值是 2 ，左边部分是 [] ，右边部分是 [1] 。
            - 空数组，无子节点。
            - 只有一个元素，所以子节点是一个值为 1 的节点。
    - [0,5] 中的最大值是 5 ，左边部分是 [0] ，右边部分是 [] 。
        - 只有一个元素，所以子节点是一个值为 0 的节点。
        - 空数组，无子节点。

示例 2：

C++
1
2
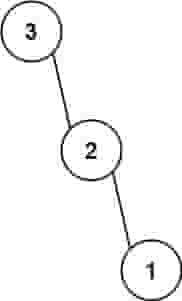
输入：nums = [3,2,1]
输出：[3,null,2,null,1]

思路分析：

  1. 解法1：常规构建

    本题思路和前序、中序以及后序、中序构建二叉树思路基本一致，只是按照某种特定的规则

  2. 解法2：单调栈

    具体见算法：单调栈篇

参考代码：

C++
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
class Solution654
{
public:
    TreeNode *constructMaximumBinaryTree(vector<int> &nums)
    {
        if (nums.size() == 0)
            return nullptr;

        // 1. 找出最大值作为根节点
        int maxRootIndex = 0;
        for (int i = 0; i < nums.size(); i++)
            if (nums[i] > nums[maxRootIndex])
                maxRootIndex = i;

        TreeNode *root = new TreeNode(nums[maxRootIndex]);

        // 2. 根据最大值分割数组（左闭右开）
        vector<int> numsLeft(nums.begin(), nums.begin() + maxRootIndex);
        vector<int> numsRight(nums.begin() + maxRootIndex + 1, nums.end());

        // 3. 构建左子树和右子树
        root->left = constructMaximumBinaryTree(numsLeft);
        root->right = constructMaximumBinaryTree(numsRight);

        return root;
    }
};

力扣617.合并二叉树

力扣617.合并二叉树

问题描述：

Quote

给你两棵二叉树：root1和root2。

想象一下，当你将其中一棵覆盖到另一棵之上时，两棵树上的一些节点将会重叠（而另一些不会）。你需要将这两棵树合并成一棵新二叉树。合并的规则是：如果两个节点重叠，那么将这两个节点的值相加作为合并后节点的新值；否则，不为null的节点将直接作为新二叉树的节点。

返回合并后的二叉树。

注意: 合并过程必须从两个树的根节点开始。

示例 1：

C++
1
2
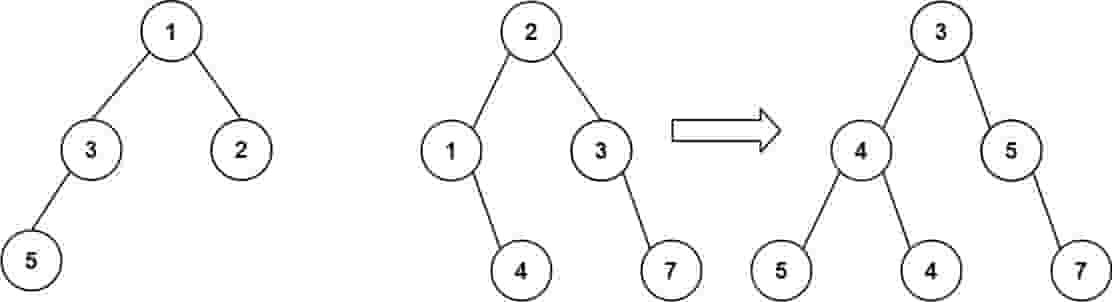
输入：root1 = [1,3,2,5], root2 = [2,1,3,null,4,null,7]
输出：[3,4,5,5,4,null,7]

示例 2：

C++
1
2
输入：root1 = [1], root2 = [1,2]
输出：[2,2]

思路分析：

本题的基本思路如下：

  1. 遍历两个树，如果两个树的同一个位置都有节点，直接累加，再遍历左子树和右子树，将结果节点链接到一棵树即可
  2. 如果其中一个树节点为空，返回另外一棵树即可
  3. 如果两个树都为空，直接返回空指针

参考代码：

C++
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
class Solution617
{
public:
    TreeNode *mergeTrees(TreeNode *root1, TreeNode *root2)
    {
        if (!root1 && !root2)
            return nullptr;
        else if (!root1)
            return root2;
        else if (!root2)
            return root1;

        root1->val += root2->val;

        root1->left = mergeTrees(root1->left, root2->left);
        root1->right = mergeTrees(root1->right, root2->right);

        return root1;
    }
};

力扣236.二叉树的最近公共祖先

力扣236.二叉树的最近公共祖先

问题描述：

Quote

给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。

百度百科中最近公共祖先的定义为：“对于有根树T的两个节点p、q，最近公共祖先表示为一个节点x，满足x是p、q的祖先且x的深度尽可能大（一个节点也可以是它自己的祖先）。”

示例 1：

C++
1
2
3
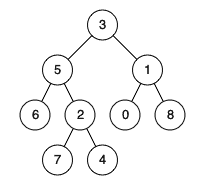
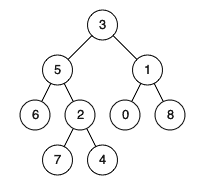
输入：root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
输出：3
解释：节点 5 和节点 1 的最近公共祖先是节点 3 。

示例 2：

C++
1
2
3
输入：root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
输出：5
解释：节点 5 和节点 4 的最近公共祖先是节点 5 。因为根据定义最近公共祖先节点可以为节点本身。
示例 3：

C++
1
2
输入：root = [1,2], p = 1, q = 2
输出：1

思路分析：

首先必须理解何为最近公共祖先，所谓祖先节点就是所有节点的父亲节点，一般指根节点，那么最近公共祖先就是最近的一个包含两个子节点的子树的根节点，其中要求深度最大，意味着如果出现一个根节点中包含了一棵子树，这棵子树的根节点包括了指定的两个子节点，那么这棵子树的根节点即为最近公共祖先，而不是子树根节点的父亲节点

理解了何为最近公共祖先，接下来就可以考虑本题的思路，本题最基本的思路就是：

  1. 同一个子树中存在p，q，则此时p或者q其中一个可能是公共祖先
  2. 不同子树中存在p，q，则此时二者的公共父亲就是公共祖先

所以现在的问题就演变为如何判断在一棵子树下： 1. 如果在p中找到q，则说明p是公共祖先，否则q是公共祖先 2. 如果p和q都是叶子节点，则找他们的公共祖先

在下面的代码中，有两种写法，第一种写法就是考虑了所有的情况，相对比较复杂，第二种情况就是在处理一般情况的同时处理了p或者q为最近公共祖先的情况，因为情况2的本质就是p和q在p或者q的子树下，那么在遍历二叉树的过程中，一定会优先查找到p或者q，此时就会返回p或者q，而因为p或者q一直是q或者p的孩子，所以在返回left或者right时只会返回其中一个，具体见代码

参考代码：

C++
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
class Solution236_1
{
public:
    // 判断是否在同一棵子树下
    bool isUnder(TreeNode *root, TreeNode *target)
    {
        if (!root)
            return false;

        if (root->val == target->val)
            return true;
        // 在该子树中找到了就返回true
        return isUnder(root->left, target) || isUnder(root->right, target);
    }

    // 遍历查找节点
    TreeNode *traversal(TreeNode *root, TreeNode *target)
    {
        if (!root)
            return nullptr;

        if (root->val == target->val)
            return root;

        TreeNode *left = traversal(root->left, target);
        TreeNode *right = traversal(root->right, target);

        if (left)
            return left;

        if (right)
            return right;

        return nullptr;
    }

    TreeNode *lowestCommonAncestor(TreeNode *root, TreeNode *p, TreeNode *q)
    {
        // 找到两个节点
        TreeNode *node1 = traversal(root, p);
        TreeNode *node2 = traversal(root, q);

        // 判断p和q是否在同一棵子树下
        if (isUnder(node1, node2)) // q在p的子树中
            return p;
        else if (isUnder(node2, node1)) // p在q的子树中
            return q;

        // 如果既不在q也不再p，直接二者共有的父亲节点
        // 思路如下：
        // 从根节点开始遍历，如果在cur->left中找到了node1和node2，说明node1和node2在cur的左子树中
        // 继续向下遍历，直到cur->left不存在node1和node2，此时cur就是共有的父亲节点
        // 如果在cur->right中找到了node1和node2，说明node1和node2在cur的右子树中
        // 继续向下遍历，直到cur->right不存在node1和node2，此时cur就是共有的父亲节点
        TreeNode *cur = root;
        while (cur)
        {
            if (isUnder(cur->left, node1) && isUnder(cur->left, node2))
                cur = cur->left;
            else if (isUnder(cur->right, node1) && isUnder(cur->right, node2))
                cur = cur->right;
            else
                break;
        }

        return cur;
    }
};
C++
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class Solution236_2
{
public:
    TreeNode *lowestCommonAncestor(TreeNode *root, TreeNode *p, TreeNode *q)
    {
        // 如果当前节点为p或者q，则直接返回当前节点
        if (root == p || root == q || root == nullptr)
            return root;

        // 后序遍历
        // 先在左子树中找p和q，如果找到了p就会一直向上返回而不会继续找q
        // 对于一般情况（即p或者q都不是最近公共祖先）来说，p和q不会存在于同一条路径下
        // 所以也就不会出现遍历左子树和右子树都遍历的是同一个值p或者q
        TreeNode *left = lowestCommonAncestor(root->left, p, q);
        // 遍历右子树找p和q
        TreeNode *right = lowestCommonAncestor(root->right, p, q);

        // 处理
        // 如果左孩子不为空，右孩子也不为空，说明当前函数栈帧的root的值就是最近公共祖先
        if (left && right)
            return root;
        else if (!left && right) // 如果左为空，右不为空，说明还没有找到最近公共祖先，只找到了一棵子树的根
            return right;
        else if (left && !right) // 同上面的情况
            return left;

        return nullptr;
    }
};

力扣606.根据二叉树创建字符串

力扣606.根据二叉树创建字符串

问题描述：

Quote

给你二叉树的根节点root，请你采用前序遍历的方式，将二叉树转化为一个由括号和整数组成的字符串，返回构造出的字符串。

空节点使用一对空括号对()表示，转化后需要省略所有不影响字符串与原始二叉树之间的一对一映射关系的空括号对。

示例 1：

C++
1
2
3
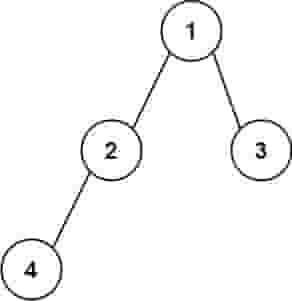
输入：root = [1,2,3,4]
输出："1(2(4))(3)"
解释：初步转化后得到 "1(2(4)())(3()())" ，但省略所有不必要的空括号对后，字符串应该是"1(2(4))(3)" 。

示例 2：

C++
1
2
3
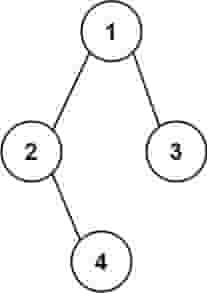
输入：root = [1,2,3,null,4]
输出："1(2()(4))(3)"
解释：和第一个示例类似，但是无法省略第一个空括号对，否则会破坏输入与输出一一映射的关系。

思路分析：

本题基本思路如下：

  1. 当前节点的左孩子和右孩子均不为空时，正常插入并正确闭合括号
  2. 当前节点的左孩子不为空，右孩子为空时，正常插入并正确闭合括号
  3. 当前节点的左孩子为空，但是右孩子不为空时，左孩子需要插入空括号对，再插入右节点

根据上面的思路可以写出第一种详细的写法，但是从上面的思路看出，其实只需要考虑最后一种情况，也就是左为空，但是右不为空时就需要额外添加左子树的括号，所以可以考虑先写出加上全部括号的逻辑再使用if划分情况，但是，第二种写法会在性能上有很大影响，因为每一次递归都会创建一个新的string对象，并且在每一次返回时都需要进行构造，导致额外的时间和空间的开销，可以考虑第一种写法，也可以考虑使用stringstream流来优化整个过程，并且使用引用防止拷贝构造

参考代码：

C++
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
class Solution606_1
{
public:
    void _tree2str(TreeNode *root, string &ret)
    {
        ret += "(" + to_string(root->val);
        if (!root->left && root->right)
            ret += "()";

        if (root->left)
            _tree2str(root->left, ret);

        if (root->right)
            _tree2str(root->right, ret);

        // 左右子树都遍历完毕后右括号首尾
        ret += ")";
    }

    string tree2str(TreeNode *root)
    {
        if (!root)
            return "";

        string ret;
        // 单独处理根节点
        ret += to_string(root->val);

        if (root->left)
            _tree2str(root->left, ret);
        else if (!root->left && root->right)
            ret += "()";

        if (root->right)
            _tree2str(root->right, ret);

        return ret;
    }
};
C++
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
class Solution606_2
{
public:
    string tree2str(TreeNode *root)
    {
        string ret;
        if (!root)
            return ret;

        // 插入节点值
        ret += to_string(root->val);

        // 左子树不为空，正常插入左子树和括号
        // 左子树为空，但右子树不为空，正常插入括号
        if (root->left || root->right)
        {
            ret += "(";
            if (root->left)
                ret += tree2str(root->left);
            ret += ")";
        }

        // 右子树不为空时，正常插入右子树和括号
        if (root->right)
        {
            ret += "(";
            ret += tree2str(root->right);
            ret += ")";
        }

        return ret;
    }
};
C++
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
class Solution 
{
public:
    // 前序遍历并构造字符串的递归函数
    void tree2str(TreeNode* root, stringstream& ss) 
    {
        if (!root) 
            return;

        // 将当前节点的值添加到字符串流中
        ss << root->val;

        // 如果有左子树或右子树（必须处理右子树为空的情况）
        if (root->left || root->right) 
        {
            ss << "(";
            tree2str(root->left, ss);
            ss << ")";
        }

        // 如果有右子树
        if (root->right) 
        {
            ss << "(";
            tree2str(root->right, ss);
            ss << ")";
        }
    }

    string tree2str(TreeNode* root) 
    {
        stringstream ss;
        tree2str(root, ss);
        return ss.str();
    }
};

力扣129.求根节点到叶节点数字之和

力扣129.求根节点到叶节点数字之和

问题描述：

Quote

给你一个二叉树的根节点root，树中每个节点都存放有一个0到9之间的数字。 每条从根节点到叶节点的路径都代表一个数字：

例如，从根节点到叶节点的路径1->2->3表示数字 123 。 计算从根节点到叶节点生成的 所有数字之和 。

叶节点 是指没有子节点的节点。

示例 1：

C++
1
2
3
4
5
6
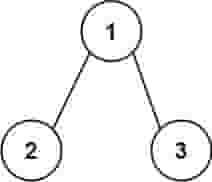
输入：root = [1,2,3]
输出：25
解释：
从根到叶子节点路径 1->2 代表数字 12
从根到叶子节点路径 1->3 代表数字 13
因此，数字总和 = 12 + 13 = 25

示例 2：

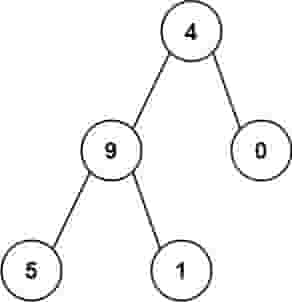
C++
1
2
3
4
5
6
7
输入：root = [4,9,0,5,1]
输出：1026
解释：
从根到叶子节点路径 4->9->5 代表数字 495
从根到叶子节点路径 4->9->1 代表数字 491
从根到叶子节点路径 4->0 代表数字 40
因此，数字总和 = 495 + 491 + 40 = 1026

思路分析：

  1. 解法1：异地处理

    通过获取所有路径插入到路径数组中，将每一条路径数组中的值组合成为一个整数，依次计算和即可

  2. 解法2：原地处理

    将上面的获取路径步骤修改为计算路径值

参考代码：

C++
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
class Solution129_1
{
public:
    void traversal(TreeNode *root, vector<vector<int>> &paths, vector<int> &ret)
    {
        if (!root)
            return;

        ret.push_back(root->val);
        if (!root->left && !root->right)
        {
            paths.push_back(ret);
            ret.pop_back();
            return;
        }

        traversal(root->left, paths, ret);
        traversal(root->right, paths, ret);

        // 遍历完所有子树后全部弹出回到根节点
        ret.pop_back();
    }

    int calculate(vector<int> &path)
    {
        int ans = 0;
        int base = 0;
        for (auto num: path)
        {
            ans = base * 10 + num;
            base = ans;
        }

        return ans;
    }

    int _sumNumbers(vector<vector<int>> &paths)
    {
        int sum = 0;
        for (auto &path: paths)
        {
            int num = calculate(path);
            sum += num;
        }

        return sum;
    }

    int sumNumbers(TreeNode *root)
    {
        vector<vector<int>> paths;
        vector<int> ret;
        traversal(root, paths, ret);

        return _sumNumbers(paths);
    }
};
C++
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
class Solution129_2
{
public:
    int traversal(TreeNode *root, int prev)
    {
        if (!root)
            return 0;

        // 计算路径值
        prev = prev * 10 + root->val;
        // 遇到叶子节点，返回当前路径值
        if (!root->left && !root->right)
            return prev;

        int sumLeft = traversal(root->left, prev);
        int sumRight = traversal(root->right, prev);

        return sumLeft + sumRight;
    }

    int sumNumbers(TreeNode *root)
    {
        int prev = 0;
        int sum = traversal(root, prev);

        return sum;
    }
};

力扣814.二叉树剪枝

问题描述：

Quote

给你二叉树的根结点root，此外树的每个结点的值要么是0，要么是1。

返回移除了所有不包含1的子树的原二叉树。

节点node的子树为node本身加上所有node的后代。

示例 1：

C++
1
2
3
4
输入：root = [1,null,0,0,1]
输出：[1,null,0,null,1]
解释：
只有红色节点满足条件“所有不包含 1 的子树”。 右图为返回的答案。

示例 2：

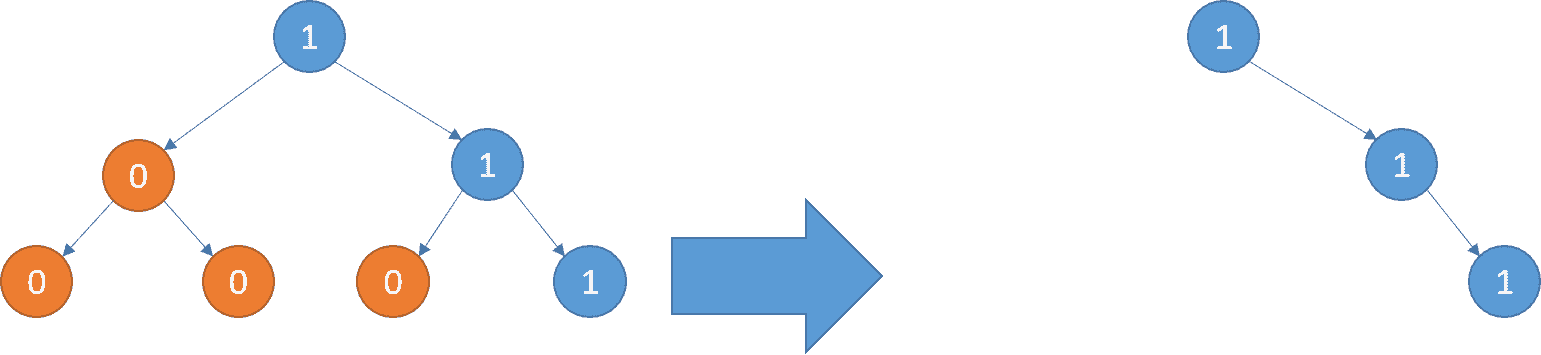
C++
1
2
输入：root = [1,0,1,0,0,0,1]
输出：[1,null,1,null,1]

示例 3：

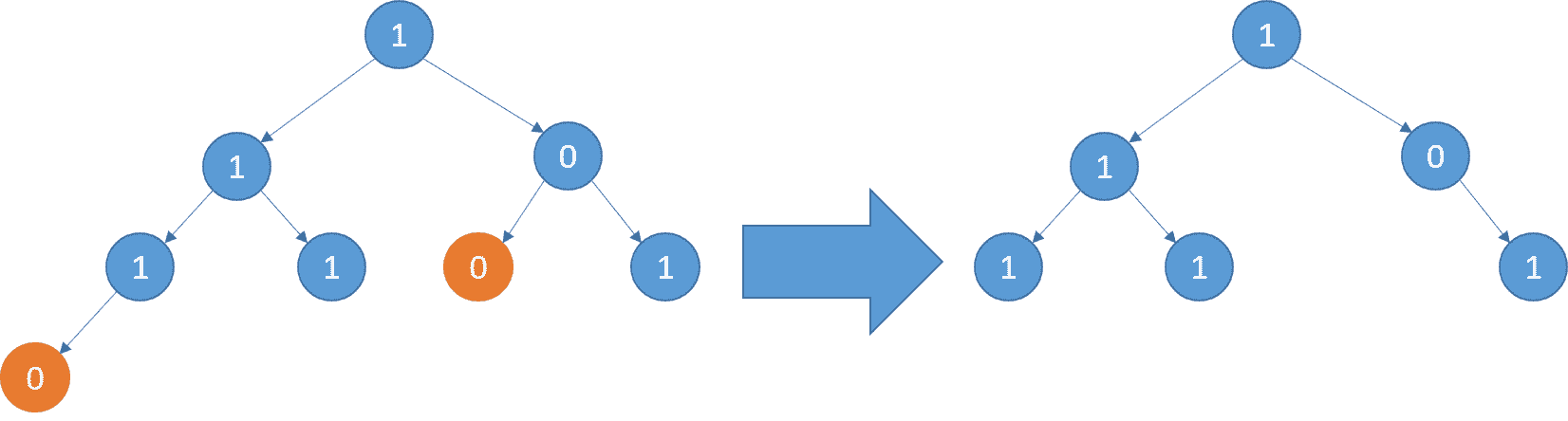
C++
1
2
输入：root = [1,1,0,1,1,0,1,0]
输出：[1,1,0,1,1,null,1]

思路分析：

本题的思路很简单，根据题目的题意分析：如果遇到0且为叶子节点，就删除该节点，否则不处理。因为要判断一个节点是否是叶子节点，就必须先获取到左右子树的信息，所以就需要后序遍历，删除节点后，向上层返回空，上层需要使用节点的left或者right接收

关键步骤：

注意，本题不要使用delete，面试时对于可能需要用到delete时，一定要询问面试官树的节点是否是在堆上开辟的空间

参考代码：

C++
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution814
{
public:
    TreeNode *pruneTree(TreeNode *root)
    {
        if (!root)
            return nullptr;

        root->left = pruneTree(root->left);
        root->right = pruneTree(root->right);

        if (!root->left && !root->right && root->val == 0)
        {
            // delete root; 注意是否需要释放内存要看具体情况（一定要确定是否是在堆上开出的空间），本题不能释放
            return nullptr;
        }

        // 如果为1就返回当前子树的根
        return root;
    }
};