跳转至

大数运算

约 934 个字 299 行代码 1 张图片 预计阅读时间 7 分钟

介绍

大数运算在系统内置的一些类型无法计算出精确值或者存在溢出时常见，此时的数值就不是简单的数字字面量，一般常见的是字符串或者数组，并且提供对应的方法，例如Java中的BigtInteger类

本次介绍的大数运算一共包括下面的几种：

  1. 大数加法
  2. 大数减法

Note

因为常见的大数运算只会计算正整数，所以本次模拟实现只会考虑0及以上的数值

大数加法

大数加法主要的思路是模拟加法运算规则，先回忆加法运算的规则：

  1. 低位依次相加
  2. 进位与下一次加法一起运算
  3. 高位位数不够加时填充0再执行相加

根据上面的规则，本次通过数组进行模拟，模拟过程如下：

  1. 使用两个指针分别从后往前遍历两个数组（对应规则：低位相加）
  2. 依次在两个数组中取出对应的数值与进位一起相加，并更新两个指针（对应规则：进位与下一次加法一起运算）
  3. 相加结果是两位时，低位是结果，高位是进位，如果没有进位需要将上一次的进位清0，否则导致前面的进位继续进行运算
  4. 尾插结果到新数组中
  5. 重复上面的步骤，直到有一个数组走到结尾
  6. 走完循环后，可能存在其中一个数组还没有走完，需要继续与进位相加（对应规则：高位位数不够加时填充0再执行相加）
  7. 走完上面的步骤可能进位不为0，此时进位需要再进行一次相加操作
  8. 翻转结果数组

计算示意图如下：

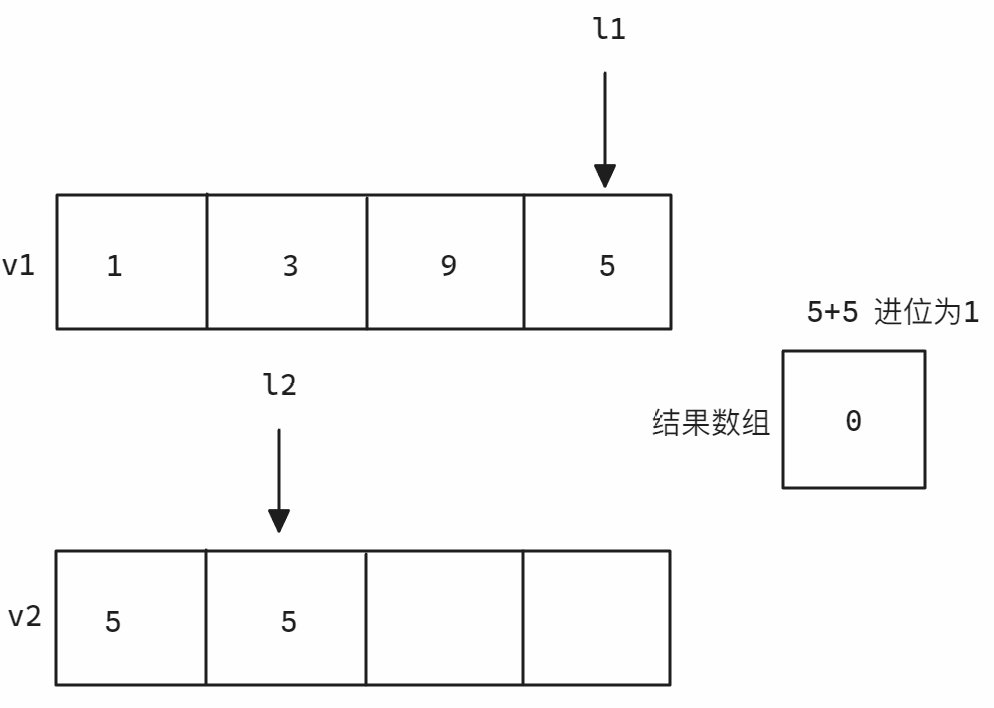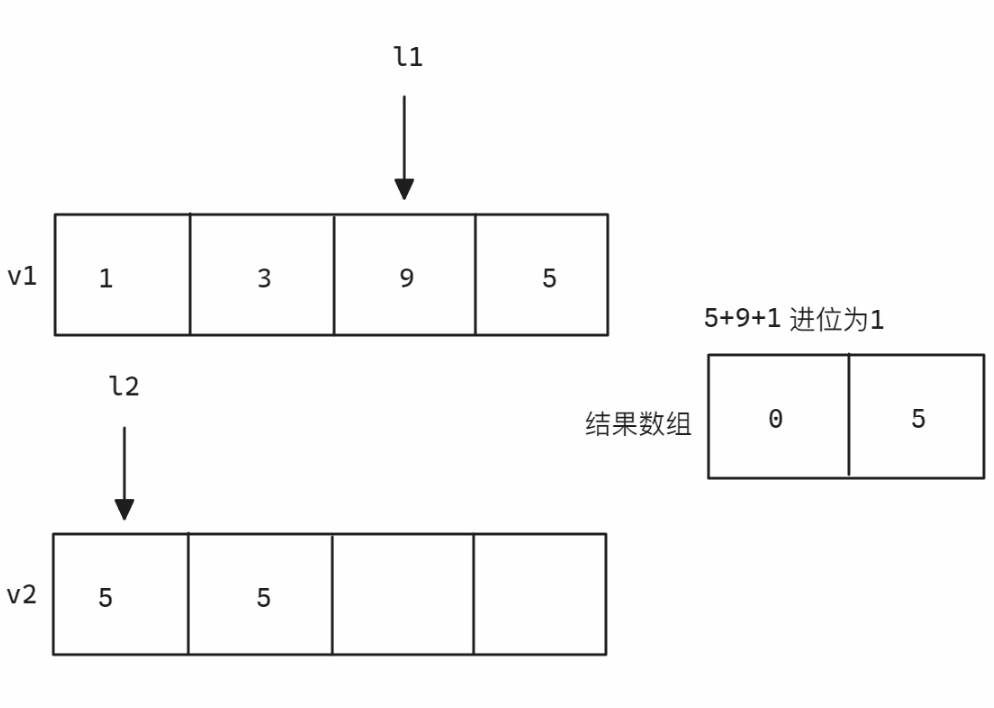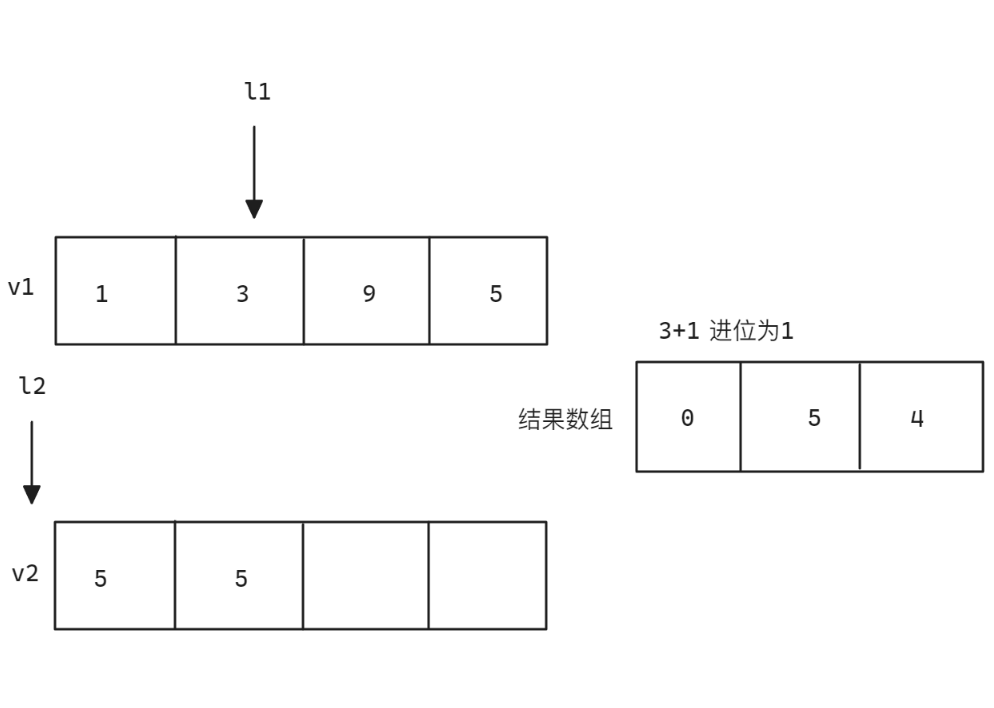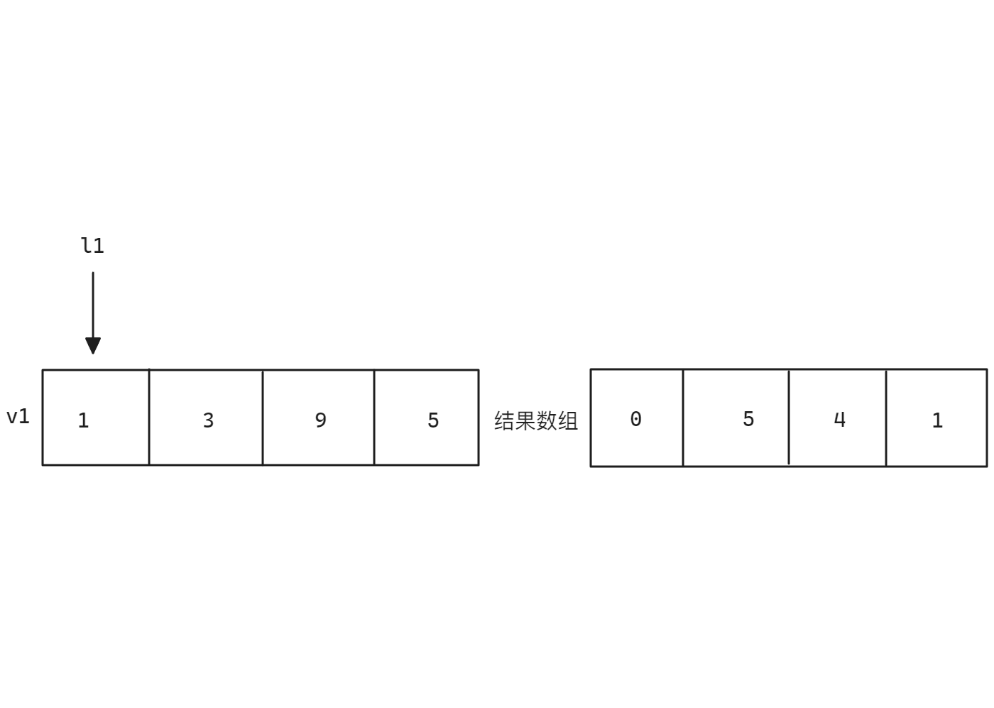
思路简化：

Note

建议先弄懂前面的代码再看简化版本的思路

简化版本本质逻辑不变，只是减少了部分重复的代码，下面是更改的位置：

  1. 相加时的循环判断逻辑

    C++
    1
2
3
4
    // 原来
while(l1 >= 0 && l2 >= 0)
// 现在
while(l1 >=0 || l2 >= 0 || carry)

  2. 取出数值求和

    C++
    1
2
3
4
5
6
    // 原来
int digit1 = v1[l1--];
int digit2 = v2[l2--];
// 现在
int digit1 = l1 < 0 ? 0 : v1[l1--];
int digit2 = l2 < 0 ? 0 : v2[l2--];

  3. 删除对单个数组的剩余部分判断以及进位的判断

参考代码：

C++
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
vector<int> add(const vector<int> &v1, const vector<int> &v2)
{
    // 取出最长的为基准
    int maxLen = v1.size() > v2.size() ? v1.size() : v2.size();

    // 处理进位
    int carry = 0;
    // 结果数组
    vector<int> ret;

    int l1 = v1.size() - 1;
    int l2 = v2.size() - 1;

    while (l1 >= 0 && l2 >= 0)
    {
        // 取出数值
        int digit1 = v1[l1--];
        int digit2 = v2[l2--];

        // 计算加法
        int sum = digit1 + digit2 + carry;
        ret.push_back(sum % 10);
        if (sum / 10)
        {
            carry = sum / 10;
        }
        else
        {
            carry = 0;
        }
    }

    // 判断最后是否还有一个未走完以及是否有进位
    while (l1 >= 0)
    {
        int sum = v1[l1--] + carry;
        if (sum / 10)
        {
            carry = sum / 10;
        }
        else
        {
            carry = 0;
        }
        ret.push_back(sum % 10);
    }

    while (l2 >= 0)
    {
        int sum = v2[l2--] + carry;
        if (sum / 10)
        {
            carry = sum / 10;
        }
        else
        {
            carry = 0;
        }
        ret.push_back(sum % 10);
    }

    // 判断最后是否有进位
    if (carry)
    {
        ret.push_back(carry);
    }

    reverse(ret.begin(), ret.end());

    return ret;
}
C++
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
vector<int> add1(const vector<int> &v1, const vector<int> &v2)
{
    // 处理进位
    int carry = 0;
    // 结果数组
    vector<int> ret;

    int l1 = v1.size() - 1;
    int l2 = v2.size() - 1;

    while (l1 >= 0 || l2 >= 0 || carry)
    {
        // 取出数值
        int digit1 = l1 >= 0 ? v1[l1--] : 0;
        int digit2 = l2 >= 0 ? v2[l2--] : 0;

        // 计算加法
        int sum = digit1 + digit2 + carry;
        ret.push_back(sum % 10);
        carry = sum / 10;
    }

    reverse(ret.begin(), ret.end());

    return ret;
}

大数减法

大数减法主要的思路是模拟减法运算规则，先回忆减法运算的规则：

  1. 低位依次相减
  2. 被减数小于减数时，向前一位借位
  3. 减数高位已经没有时填充0再执行相减

根据上面的规则，本次通过数组进行模拟，模拟过程如下：

  1. 判断两个数组的长度，本次模拟实现中第一个数组为被减数，第二个数组为减数，如果第一个数组较小，则交换位置再调用函数，否则直接继续
  2. 使用两个指针分别从后往前遍历两个数组（对应规则：低位相减）
  3. 取出对应的数值结合借位进行减法运算，如果结果小于0，说明当前存在借位情况。这里处理的方式实际上是让小于0的数值回转到大于等于0即可，所以在可以借位的减法中，例如4-6就是14-6，其本质就是10+4-6，只需要让小于0的结果加10即可，并记录当前已经进行一次借位，下一次运算时需要减掉这个借位
  4. 减法存在前导0的情况，所以需要取出前导0
  5. 最后翻转结果数组即可

参考代码：

C++
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
// 大数减法
vector<int> sub(vector<int> &v1, vector<int> &v2)
{
    if(v1.size() < v2.size())
    {
        return sub(v2, v1);
    }

    // 结果数组
    vector<int> ret;
    int carry = 0;

    int l1 = v1.size() - 1;
    int l2 = v2.size() - 1;

    while (l1 >= 0 || l2 >= 0)
    {
        int digit1 = (l1 >= 0) ? v1[l1] : 0;
        int digit2 = (l2 >= 0) ? v2[l2] : 0;

        int sub = digit1 - digit2 - carry;
        if (sub < 0)
        {
            sub += 10;
            carry = 1;
        }
        else
        {
            carry = 0;
        }

        ret.push_back(sub);
        l1--;
        l2--;
    }

    // 移除前导零
    while (ret.size() > 1 && ret.back() == 0)
    {
        ret.pop_back();
    }

    // 反转回正确的顺序
    reverse(ret.begin(), ret.end());

    return ret;
}

大数乘法（简单了解）

参考代码：

C++
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
// 大数乘法
// 假设 v1 和 v2 都表示非负整数，且每个元素为一个数字（0-9），最高位在前
vector<int> multiply(vector<int> &v1, vector<int> &v2)
{
    int n1 = v1.size();
    int n2 = v2.size();
    // 初始化结果向量，最大可能长度为 n1 + n2
    vector<int> result(n1 + n2, 0);

    // 反转两个向量以便从最低位开始计算
    vector<int> num1 = v1;
    vector<int> num2 = v2;
    reverse(num1.begin(), num1.end());
    reverse(num2.begin(), num2.end());

    // 逐位相乘并累加到结果向量
    for(int i = 0; i < n1; ++i){
        for(int j = 0; j < n2; ++j){
            result[i + j] += num1[i] * num2[j];
            // 处理进位
            if(result[i + j] >= 10){
                result[i + j + 1] += result[i + j] / 10;
                result[i + j] %= 10;
            }
        }
    }

    // 处理可能的进位
    for(int i = 0; i < result.size() - 1; ++i){
        if(result[i] >= 10){
            result[i + 1] += result[i] / 10;
            result[i] %= 10;
        }
    }

    // 移除结果中的前导零
    while(result.size() > 1 && result.back() == 0){
        result.pop_back();
    }

    // 反转回正确的顺序
    reverse(result.begin(), result.end());

    return result;
}

大数除法（简单了解）

参考代码：

C++
  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
// 辅助函数：比较两个大数（向量表示），返回1表示num1 > num2，0表示相等，-1表示num1 < num2
int compare_vectors(const vector<int> &num1, const vector<int> &num2) {
    if (num1.size() > num2.size()) return 1;
    if (num1.size() < num2.size()) return -1;
    for (size_t i = 0; i < num1.size(); ++i) {
        if (num1[i] > num2[i]) return 1;
        if (num1[i] < num2[i]) return -1;
    }
    return 0;
}

// 辅助函数：从向量中删除前导零
void remove_leading_zeros(vector<int> &num) {
    while (num.size() > 1 && num[0] == 0) {
        num.erase(num.begin());
    }
}

// 辅助函数：大数减法，假设num1 >= num2
vector<int> subtract_vectors(const vector<int> &num1, const vector<int> &num2) {
    vector<int> result;
    int carry = 0;
    int n1 = num1.size();
    int n2 = num2.size();

    for(int i = 1; i <= n1; ++i){
        int digit1 = num1[n1 - i];
        int digit2 = (i <= n2) ? num2[n2 - i] : 0;
        int sub = digit1 - digit2 - carry;
        if(sub < 0){
            sub += 10;
            carry = 1;
        }
        else{
            carry = 0;
        }
        result.push_back(sub);
    }

    // 移除前导零
    while(result.size() > 1 && result.back() == 0){
        result.pop_back();
    }

    // 反转回正确顺序
    reverse(result.begin(), result.end());
    return result;
}

// 辅助函数：大数乘以单一数字（0-9）
vector<int> multiply_vector_by_digit(const vector<int> &num, int digit){
    vector<int> result;
    int carry = 0;
    for(int i = num.size() -1; i >=0; --i){
        int temp = num[i] * digit + carry;
        carry = temp / 10;
        result.push_back(temp % 10);
    }
    if(carry){
        result.push_back(carry);
    }
    // 反转回正确顺序
    reverse(result.begin(), result.end());
    return result;
}

// 大数除法
// 返回商
vector<int> divide(const vector<int> &dividend, const vector<int> &divisor) {
    // 特殊情况处理
    if(divisor.size() == 1 && divisor[0] == 0){
        throw invalid_argument("除数不能为零。");
    }

    // 如果被除数小于除数，商为0
    if(compare_vectors(dividend, divisor) < 0){
        return {0};
    }

    vector<int> quotient;
    vector<int> remainder;

    for(auto digit : dividend){
        // 将当前位加入余数
        remainder.push_back(digit);
        remove_leading_zeros(remainder);

        // 找出当前余数能包含除数的最大倍数（0-9）
        int q = 0;
        while(compare_vectors(remainder, divisor) >= 0){
            remainder = subtract_vectors(remainder, divisor);
            q++;
        }
        quotient.push_back(q);
    }

    // 移除商中的前导零
    remove_leading_zeros(quotient);
    return quotient;
}